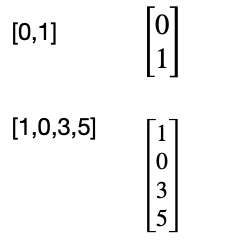
When programming, we tend to think of vectors as lists of numbers, [0,1], [1,0,3,5]

We may have seen the maths notation like this:

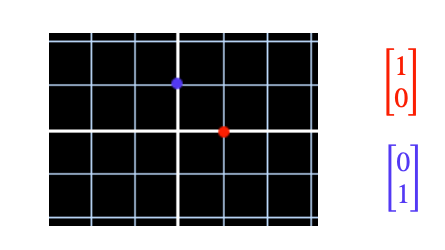
Or as points in space, if we are dealing with images, but we can also think of them as pointing in directions.

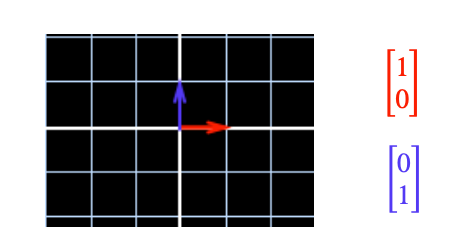
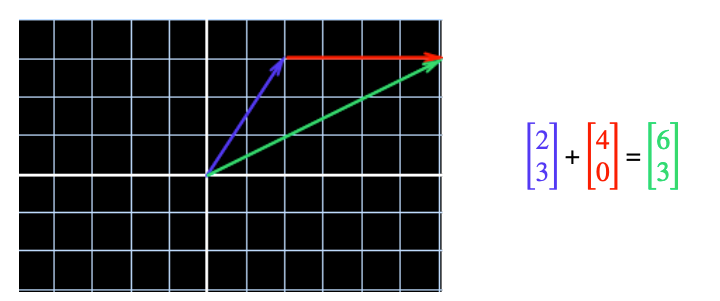
We can add them together:

And this also makes sense in space:

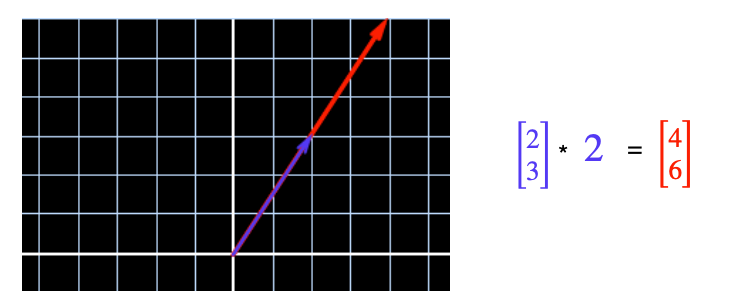
We can multiply:

And this also makes sense in space:

Linear transformations:

• Lines remain lines (not curved)
• Origin remains fixed
• Grid lines remain parallel and evenly spaced

Scale, shear, rotation, reflection

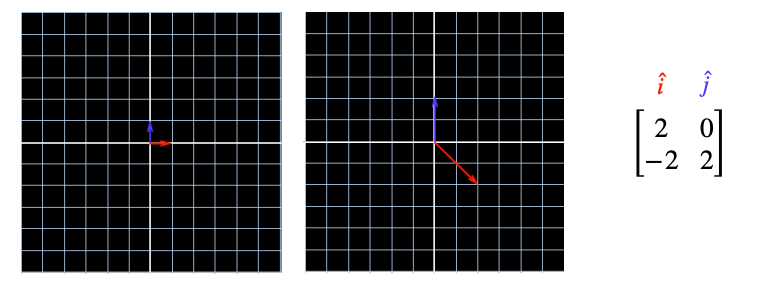
These two particular vectors of length 1 about the origin on the x and y axis are known as basis vectors.

We have seen matrices as 2D lists of numbers (like images!)

We can describe any linear transformation by providing a matrix which dictates where i and j are translated to.

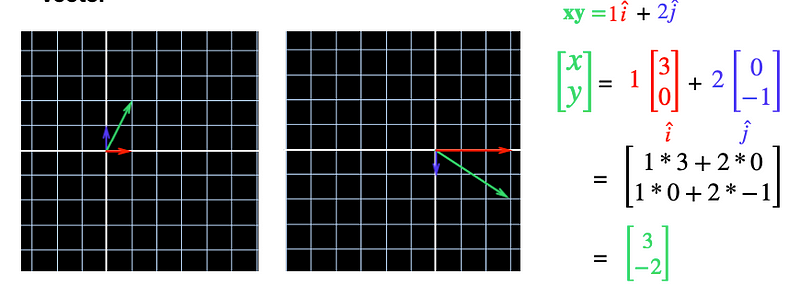
We can think of any vector as a combination of i and j. So if we translate i and j by a certain amount, we can apply that to any vector.

So given any vector[x,y] and transformation matrix we know:

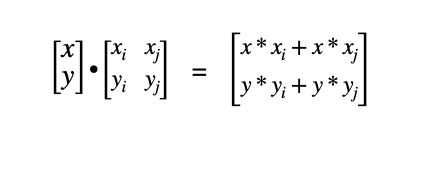
Given us the new vector after the transformation.

So what does this mean for iamges?

Every image is just a set of points.

When we translate by some matrix, we now know how to translate each point!

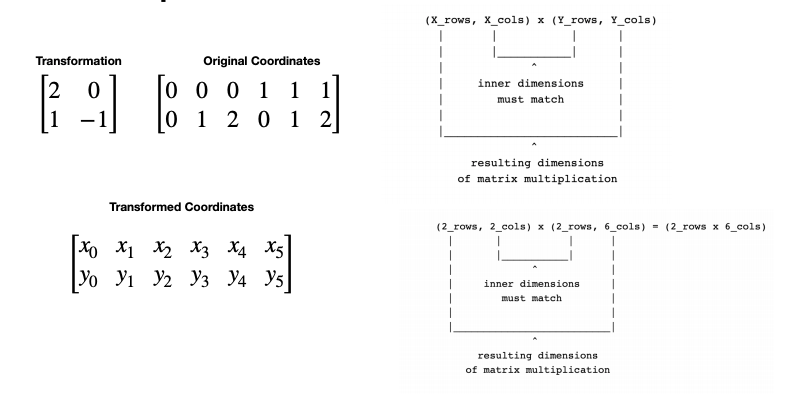
We take all the coordinates of the image, and apply the transform to them.

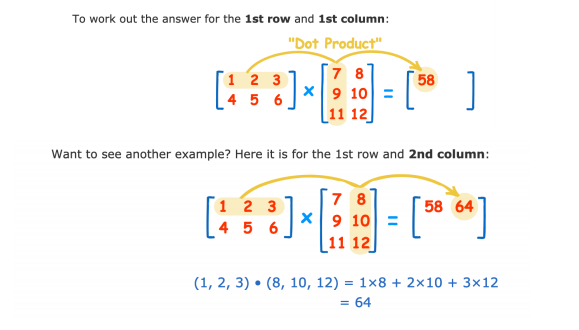
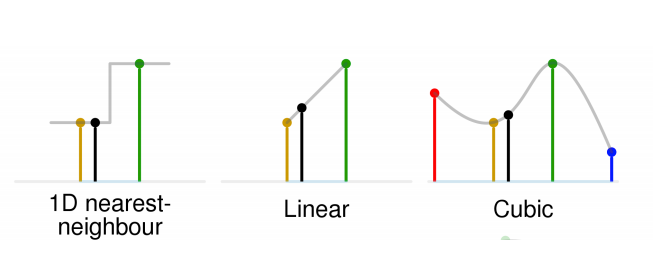
Interpolation is a set of techniques for estimating missing data.

When we were resamping audio, this is what was happening.

Resampled to play back at a higher sample rate, we need to fill in the gaps.

For Linear Interpolation -> We can use trigonometry -> SOHCATOA

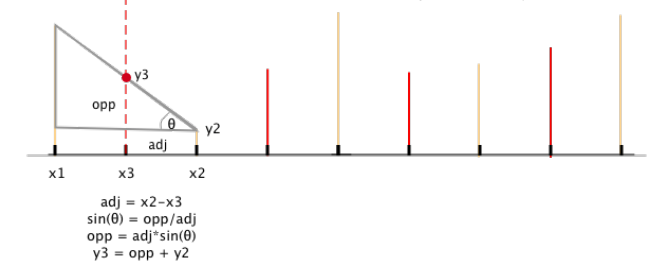
Also works in 2D, which is what we need for the transformed images.

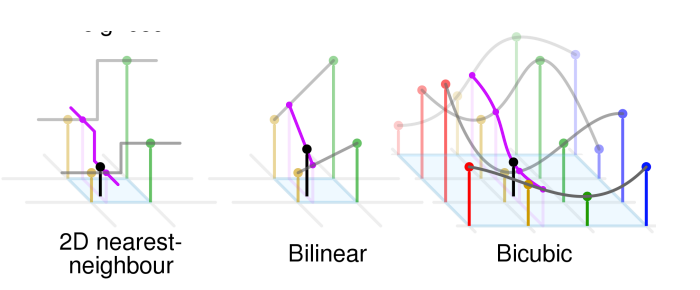
We take the original images coordinates, transform them to get new ones.

Then we take the pixel values from the oriinal image and remap them onto the new coordinates.

Looking at the transformation [2 0 |0 1], which is a stretch in the x axis, we can see that once we have shifted the values we know about onto the new coordinates, we are left with gaps in between columns that we have no direct mapping for:

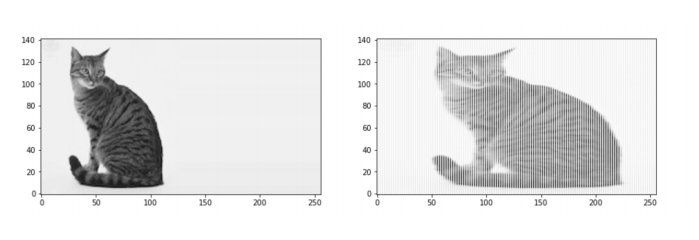
We can use interpolation to fill in the gaps!

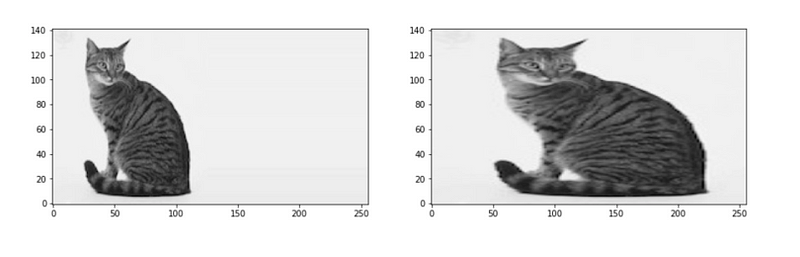
This also applies if we are left with new coordinates that are between grid points on the original image.