Latent spaces & VAEs (pre-recorded lecture):

• Convolutions for working with image data and Convolutional Neural Networks

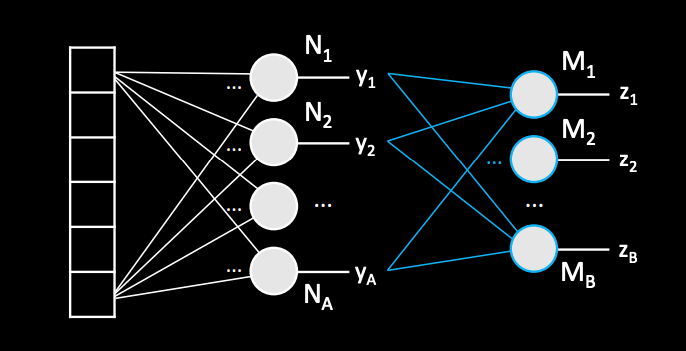
Fully-connected neuron layers: Each neuron in its layer will be connected to every output of the previous layer.

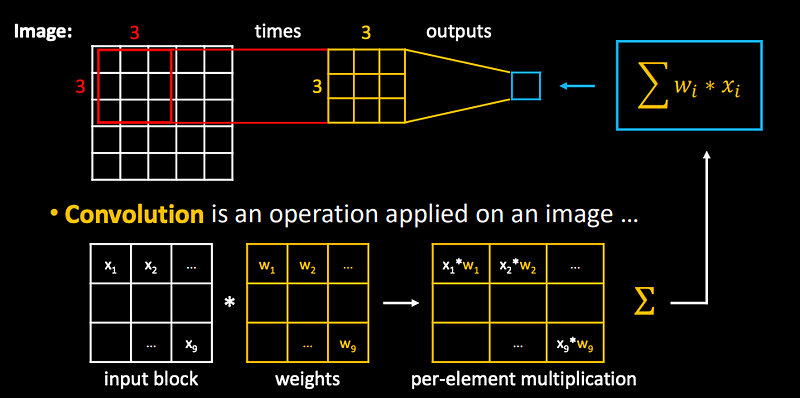
Convolution: is an operation applied on an image.

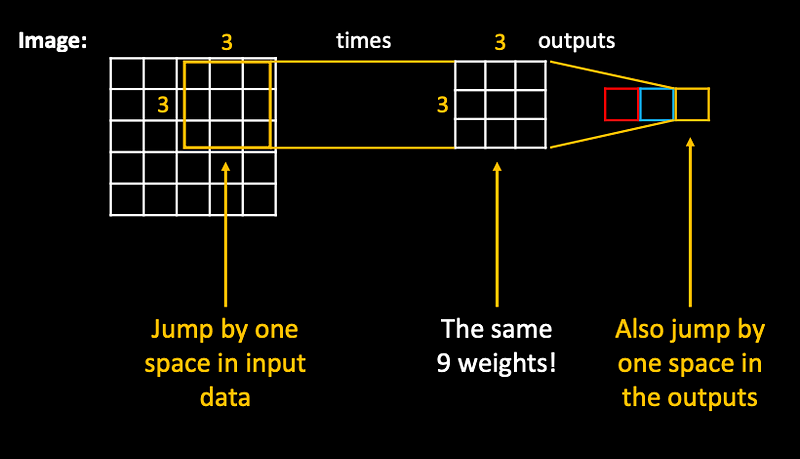
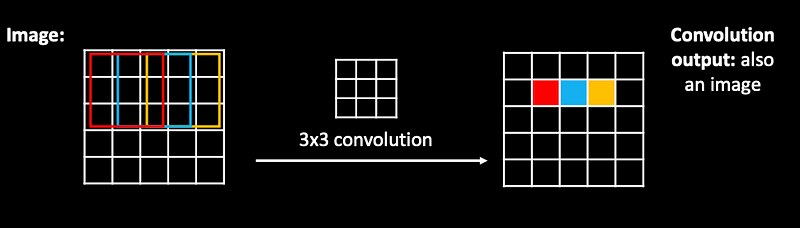
The same weights are applied as a filter, jumping over the whole image…effectively producing an image on the output!

Convolutions were used before neural networks as transformation functions to process images.

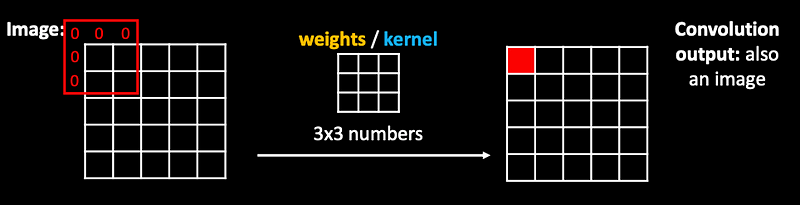
Terminology: we called these 3x3 numbers “weights”, but with convolutions they are also referred to as kernel.

Detail: to kepp the same size of the output image, we need to extend the original image by 1 pixel - we pretend that it includes zeros (also called “zero padding”).

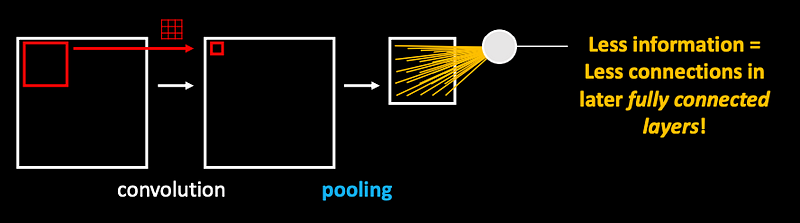
Convolutional layers are usually followed by downsampling layers (pooling) which rescale the image (less information).

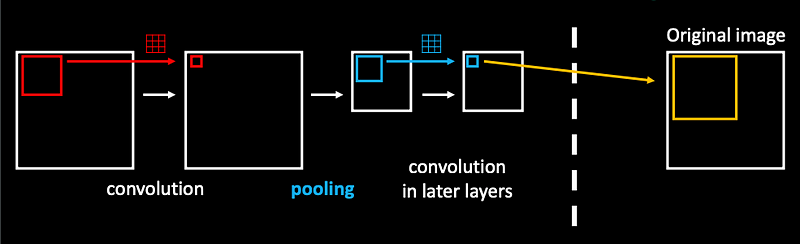
“Later” convolutions are also looking at much larger region in the original image with their kernel (receptive field).

This means, that the later convolutional layers can specialize on processing different scales of the image.

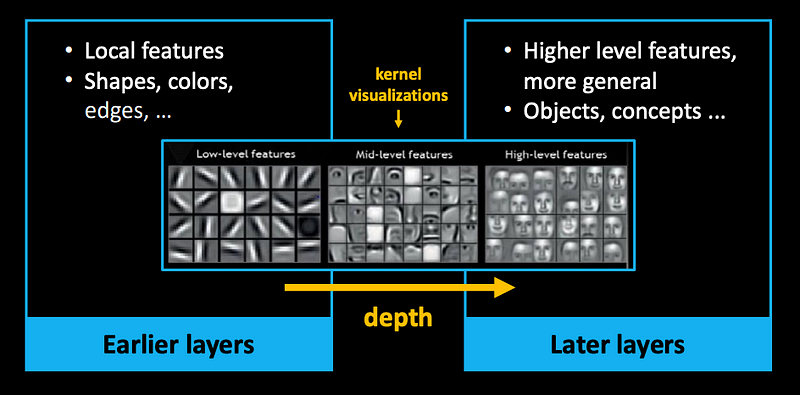
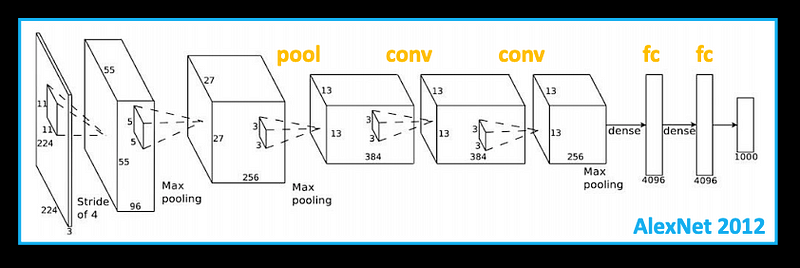
By now, we know most of the layers used in this CNN architecture! (one more detail: the Dropout layers)

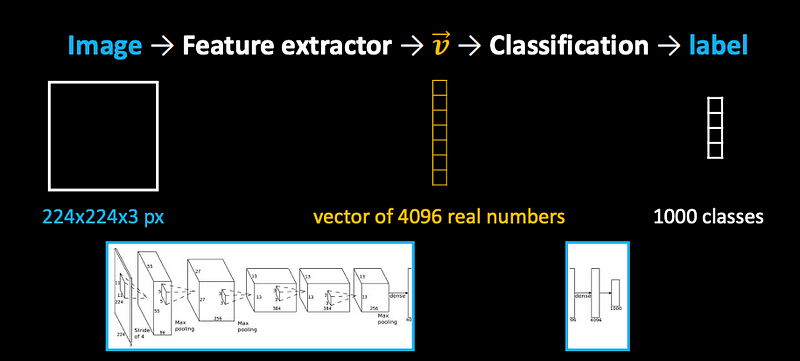
This part of the model becomes useful as a general feature extractor (its learned representation-ability is data driven - depends on the dataset!)

General feature description

Image -> Feature extractor -> Classification -> label

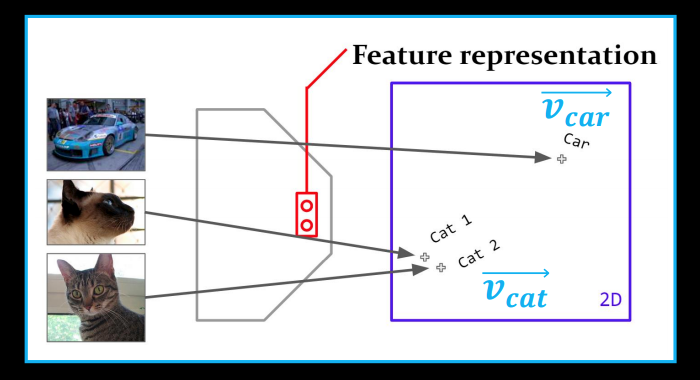
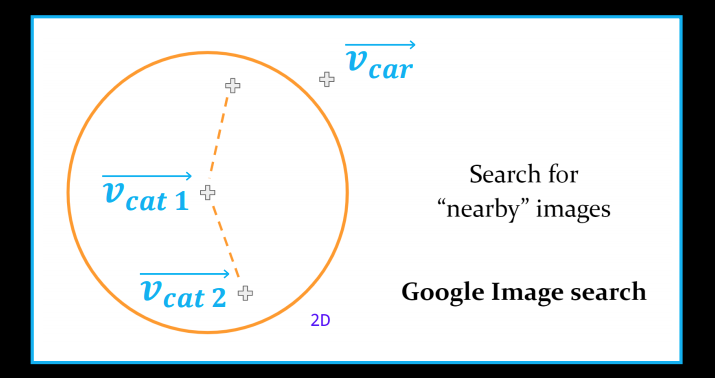
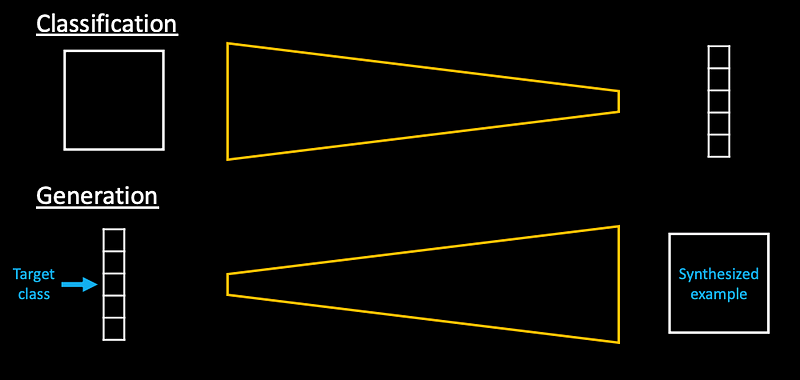
What we more or less want is flip the task - but it turns out this is too difficult task.

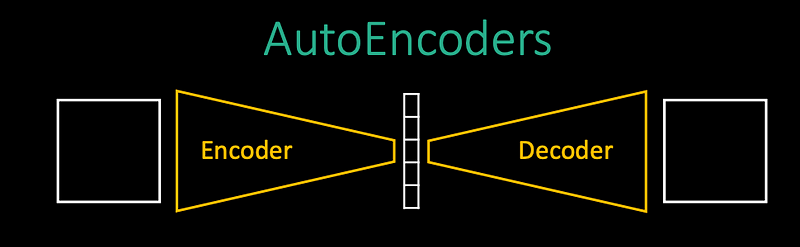
Rephrase it as an identity operation, we want the model to encode image into some intermediate lower-dimensional representation and decoder to undo that work.

Seemingly this is a useless task - we are making a machine for nothing. But as we saw in previous part (feature extraction), parts of the models can also be useful!

Encoding real samples into their latent representations.

Then using these, we can generate interpolations.

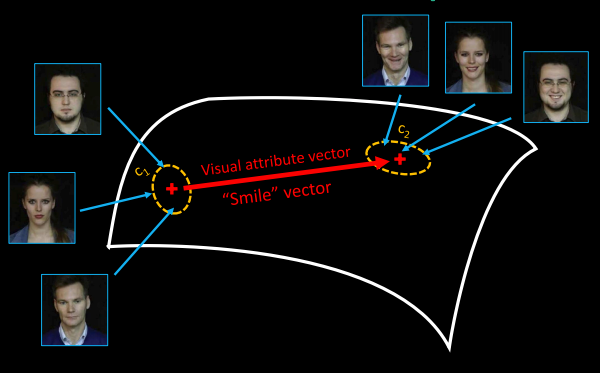
This is a high dimensional space (like a cloth shape in 3D, but in 512D instead), in which we can explore relations between data.

Each point in this space is a vector of 512 numbers (and so each point is an encoded real sample - and can also be used to generate an image).

If we encoded images with some property and without this property (for example: smiling / neutral expression)…

We can find clusters and check their relative positions:

v = centroid of c1 - centroid of c2

With labeled datasets we can extract visual attribute vectors.

we can call this latent space arithmetic.

When we need an arbitrary feature extractor / transformer of image -> feature.

• If we had labels (supervised scenario), we could used something similar like AlexNet…
• Without labels (unsupervised scenario) we can instead use these methods - Aesops or GANs.

Intuition: if the encoder can create a “good enough” representation, that it can be used for reconstruction -> then we hope that it will be good in other scenarios as well.

Reinterpret material with shapes/details/imagery of another material.

Additional readings:

Convolutional Neural Networks

• Convnets on ML4A: ml4a.github.io/ml4a/convnets/

• Interactive Convolutional Neural Network (runs in the browser and has good visualization): cs.cmu.edu/~aharley/vis/conv/flat.html

AutoEncoders

• Details about types of VAEs: lilianweng.github.io/lillog/2018/08/12/from-autoencoder-to-beta-vae.html
• VAE visualizations of latent space: hackernoon.com/latent-spacevisualization-deep-learning-bits-2-bd09a46920df